Matematik för årskurs 7-9/Geometri/3D-geometri

När man räknar volymer är det precis som när man räknar med areor viktigt att man använder samma måttenhet på alla mått. Så om en låda är 50 cm hög, 7 dm djup och 1 meter lång måste man välja vilken enhet man vill använda och göra om alla andra enheter till den INNAN man räknar ut volymen.

En liter har man bestämt att det är samma sak som en dm³. Därför kan det vara smidigt att använda just dm eftersom svaret då blir i liter. På samma sätt blir svaret i ml om man i stället använder cm när man räknar.

Enheten när man skriver ut volym har en liten upphöjd trea efter sig. Det är eftersom man har tagit enheten för lägnd och multiplicerat tre gånger. Då blir enheten upphöjd i tre. Mer om upphöjt i kan du läsa i potenskapitlet.

Enheter

Lägndenhet	Volymenhet	Alternativ volymenhet
kilometer (km)	kubikkilometer (km3)
meter (m)	kubikmeter (m3)
decimeter (dm)	kubikdecimeter (dm3)	liter (l)
centimeter (cm)	kubikcentimeter (cm3)	milliliter (ml)
millimeter (mm)	kubikmillimeter (mm3)	mikroliter (µl)

Rätblock

Volym

$V=B\cdot h$

$V=a\cdot b\cdot c$

För att beräkna volymen av ett rätblock multiplicerar man bottenarean (B i formeln ovan) med höjden (h). Eftersom bottenarean är en rektangel på ett rätblock så kan man också räkna ut volymen genom att multiplicera alla sidorna med varandra (a, b och c).

Area

$A=2\cdot a\cdot b+2\cdot a\cdot c+2\cdot b\cdot c=2(ab+ac+bc)$

För att beräkna arean på ett rätblock måste man beräkna arean på varje sida och sedan addera alla sidorna.

Övningsuppgifter

Grund-nivå

1. Beräkna volymen hos lådorna.

a)

b)

2. En tärning är formad som en kub. Träningen är 2 cm på varje sida. Beräkna tärningens volym.

3. En kartong är 4 dm bred, 5 dm lång och 4 dm djup.

a) Beräkna arean på botten och toppen.

b) Beräkna arean på framsidan och baksidan.

c) Beräkna arean på kanterna.

d) Hur stor är hela arean?

4. Kuben är 2 cm x 2 cm x 2 cm.

a) Beräkna arean på en sida.

b) Beräkna hela kubens volym.

5. En låda är 3 dm bred, 4 dm lång och 2 dm hög.

a) Beräkna lådans volym.

b) Hur många liter rymmer lådan?

6. Ett gammalt rockband heter 10 cc. Ge förslag på längd, bredd och höjd som blir 10 cm³ (cc = cubic centimeters = cm³)

E-nivå

7. Ett mjölkpaket är 7 cm x 7 cm x 20 cm.

a) Gör om måtten till dm.

b) beräkna volymen.

c) Hur många liter rymmer mjölkpaketet?

8. Hur många liter rymmer ett akvarie som är 8 dm långt, 2,5 dm djupt och 2,5 dm högt?

9. Tärningarna är 1,5 cm stora. Beräkna deras volym.

10. Hur hög behöver en fyrkantig burk vara som ska rymma 4 liter om den har bottenarean 2 dm²?

11. Ge förslag på mått till en låda som rymmer 6 liter.

12. I bilden är a = 4 cm, b = 1,5 cm och c = 3 cm.

a) Beräkna volymen.

b) Beräkna arean.

13. Hur många tegelstenar behövs för att mura en 5 meter lång vägg som är 2,5 meter hög och 20 cm tjock? En tegelsten har måtten 5x10x20 cm.

14. En vanlig svensk tegelsten brukar vara 250 x 120 x 62 mm.

a) Beräkna volymen i dm³.

b) Vad borde tegelstenen väga om den har en densitet på 2 kg/dm³.

15. Hur många kuber med sidlängden 2 cm kan man göra av en kub med sidlängden 6 cm?

16. Bilden till höger visar en 2-tum-4 planka som är 2 m lång. Den har alltså måtten 2 tum x 4 tum x 2 meter. Beräkna plankans volym. (1 tum=2,54 cm)

17. Hur många kulor består kuben på bilden av?

18. Skriv en förklarande bildtext till bilden som förklarar de olika siffrorna.

19. Hur stor är en kub som har volymen 27 dm³?

20. Beräkna area och volym.

21. Beräkna volymen i följande figurer

a)

b)

c)

d)

C-nivå

22. En järnvägsräls ser ut som nedan

a) Beräkna dess volym

b) Järn har en densitet på 7,9 kg/dm³. Vad väger rälsen?

23. Ett rum är 6 m x 8 m och det är 2,5 m till taket.

a) beräkna hur mycket luft som finns i rummet.

b) Hur länge räcker den luften tills all luft andats i medel en gång till en klass med 30 elever som tar ett andetag på en liter varannan sekund.

24. A = 1 dm², l = 1,5 m. Beräkna volymen.

25. Beräkna volymen av figuren på bilden. Antag att den är 1 meter och består av 20 cm tjocka delar.

26. Arean på en av de små kuberna är 24 cm². Vad är arean på den stora kuben?

27. En kub har en area är 54 cm². Vad är dess volym?

28. En kub har en volym på 8 cm³. Vad har den för area?

29. Jämför följande figurs area och volym med en "hel" kub som är lika stor.

a) Hur skiljer sig arean?

b) Hur skiljer sig volymen?

A-nivå

30. Hos en glasmästare tar de betalt per volym glas man köper. Antag att du ska köpa glas till ett akvarium som har yttermåtten 60 cm x 30 cm x 30 cm. Glaset ska vara 1 cm tjockt.

a) Hur mycket glas går åt?

b) Om måtten är innermått, hur mycket glas går då åt?

31. En låda görs av en kartongbit som bilden visar. Kantbitarna är dubbelt så breda som höga. Kartongen är 1 m x 80 cm.

a) Beräkna lådans mått.

b) Beräkna lådans volym.

32. Ett rätblock har förhållandet mellan sina sidor som 2

3:4.

a) om volymen är 192 cm³, vad är då dess mått?

b) om arean är 468 cm², vad är då dess mått?

33. En kub har utskärda hål likt den nedan. Kuben är 4 cm lång på alla sidor och hålet är 2 cm.

a) Beräkna Kubens volym.

b) Beräkna hur stor del av kuben utan utskärda hål som är kvar som ett bråk.

c) Bevisa att det blir samma bråk i c-uppgiften oavsett hur stor kuben är givet att hålet alltid är hälften så stort som hela sidan. (Använd 4x som lägnden på sidan)

34. Ett rätblock är lika högt som brett och dubbelt så långt som brett. Arean är 40 cm². Beräkna volymen.

Fördjupning

35. Mengers tvättsvamp

Mengers tvättsvamp skapas genom att man delar varje sida i tre delar så att den blir lik en rubiks kub. Sedan tar man bort den mittersta biten på varje sida och den biten i mitten av kuben. Sedan upprepar man detta med varje bit som är kvar så att det blir mindre och mindre bitar kvar.

a) Hur stor del av volymen från den ursprungliga kuben är kvar efter att man upprepat proceduren en gång?

b) Skriv ett uttryck med potens för hur stor del av kuben som är kvar efter man gjort proceduren n gånger. Tänk på att x⁰=1 och att x¹ ska bli svaret på a-uppgiften.

c) Hur stor area har den ursprungliga kuben om den har sidlägnden 1?

d) Hur stor area har kuben efter man gjort proceduren en gång?

Mer om mengers tvättsvamp: wikipedia

Ej nivåsatt

(Inga uppgifter här. Lägg gärna till några!)

Mall:Matematik för årskurs 7-9/Göm slut

Prismor

Volym

$V=B\cdot h$

För att beräkna volymen av ett prisma multiplicerar man bottenarean (B i formeln ovan) med höjden (h). Denna formel gäller oavsett hur prismat är format så länge som den har samma form hela vägen från botten till toppen. Så ett prisma kan ha hur många sidor som hellst (inte bara tre som i figuren) och formeln fungerar ändå så länge man vet basarean. Samma formel gäller ju i specialfallet med ett rätblock också.

Area

Arean på ett prisma kan man inte ställa upp en färdig formel för eftersom den beror på hur prismat ser ut. Vad man måste göra är att beräkna arean på varje sida och sedan addera alla de areorna.

Övningsuppgifter

Grund-nivå

1. Prismat på bilden har en bottenarea på 10,4 cm² och är 2 cm hög.

Beräkna dess volym.

E-nivå

2. Prismat på bilden har en bottenarea på 2.7 cm², är 3 cm hög och varje sida har en area på 7,5 cm².

a) Beräkna dess volym.

b) Beräkna dess area

3. Pentagonen på bilden har en bottenarea på 15,5 cm². Den är 2 cm hög. Beräkna dess volym.

4. Ett tält är triangelformat och är 2,20 m långt, 1,60 m brett och 1,20 m högt.

a) Hur många m² tältduk består tältet av?

b) Hur många m³ luft innehåller tältet?

5. På bilden är ett prisma. Den skuggade arean är 2 cm2 och den är 2 cm hög. Beräkna volymen.

6. En hexagons area är ungefär dess sidlägnd i kvadrat multiplicerat med 2,6. Hexagonen på bilden har en sidlägnd och höjd på 3 cm.

a) Beräkna volymen.

b) Beräkna arean.

C-nivå

7. Längs en väg ska ett dike grävas som är V-format. Diket ska vara 1,2 m brett och 80 cm djupt. Vägen är 400 meter lång. Hur mycket jord måste grävas bort?

8. En järnvägsräls ser ut som nedan

a) Beräkna dess genomskärningsarea

b) Beräkna dess volym

9. En verklig räl visas nedan

a) Skissa upp dess genomskärningsarea med "verkliga" mått

b) beräkna dess volym

10. Göta älv är Sveriges största flod med ett medelflöde på 570 m³/s. Om Göta älv på ett ställe är 100 m bred på 60 m av de 100 är den 8 m djup. En ungefärlig skiss av dess genomskärning visas. Hur fort rinner vattnet där? (Antag att vattnet rinner lika fort vid bottnen som vid ytan)

11. Prismat på bilden är 5 cm lång, 4 cm bred och 3 cm hög. I toppen är den hälften så bred som i botten. Beräkna volymen.

Fördjupning

Samma formel för att räkna på prismor som gäller oavsett hur basytan är formad gäller faktiskt också även om höjden inte går rakt upp så länge som genomskärningsytan är likadan hela vägen. Jämför med ett paralellogram där man kan räkna med basen gånger höjden trots att parallellogramet inte går rakt upp. Samma sak gäller här.

Man kan också tänka att man skivar prismat i väldigt tunna skivor som man sedan lägger i en rak hög så att man får ett vanligt prisma. Den metoden kallas integration och kommer användas mycket mer i gymnasiets matematik.

12. Beräkna volymen på följande figurer

a) TODO

Ej nivåsatt

Bilder till uppgifter:

Mall:Matematik för årskurs 7-9/Göm slut

Cylindrar

Volym

$V=B\cdot h$

$V=\pi \cdot r^2\cdot h$

För att beräkna volymen av en cylinder multiplicerar man bottenarean (B i formeln ovan) med höjden (h). Eftersom bottenarean är en cirkel på en cylinder så kan man också räkna ut volymen med den andra formeln där B är utbytt mot πr².

Area

$A=2\cdot \pi \cdot r\cdot h$

Arean på sidan på en cylinder beräknas genom att man tänker sig att man rullar ut den. Då får man en rektangel med längden 2πr (omkretsen på cylindern) och höjden h.

Vill man ha arean inklusive botten och toppen får man lägga till de areorna som är vanliga cirklar:

$A=2\cdot \pi \cdot r\cdot h+2\cdot \pi \cdot r^2=2\pi r(r+h)$

Övningsuppgifter

Grund-nivå

1. En cylinder har radien 5 cm och höjden 10 cm.

a) Beräkna bottenarean.

b) Beräkna volymen.

c) Beräkna diametern.

d) Beräkna omkretsen.

e) Beräkna sidans area.

f) Beräkna hela arean.

2. En cylinders har radien (r) 1 cm och höjden (h) 2 cm.

a) Beräkna bottenarean

b) Beräkna volymen

c) Beräkna omkretsen

d) Beräkna arean på sidan (det blå området)

3. En cylinder har radien 1 dm och är 2 dm hög.

a) Beräkna bottenarean.

b) Beräkna volymen.

4. Beräkna volymen hos en cylinder med radien 2 cm och höjden 5 cm.

E-nivå

5. En cylinder som på bilden har diamtern 2 cm och höjden 3 cm.

a) Beräkna volymen

b) Beräkna arean på sidan

c) Beräkna hela arean (inklusive botten och toppen)

6. Beräkna volymern hos en cylinder med diametern 25 mm och höjden 50 mm.

7. Hur mycket vatten rymmer en brunn som har diametern 1 m och där det är 3 m djupt?

8. Beräkna area och volym på en cylinder med radien 5 cm och höjden 5 cm.

9. En cylinderformad läskburk är 6,3 cm i diameter och 10,5 cm hög. Hur många cl rymmer den?

10. Hur hög ska en cylinderformad läskburk vara om den är 6,3 cm i diameter och ska rymma en halv liter?

11. Beräkna volym och area hos följande figur

bredd = 2 cm

tjocklek = 0,5 cm

hålets diameter = 1 cm

12. Ungefär hur mycket hö är det i en sådan bal som på bilden? Du får själv uppskatta balens mått.

13. Beräkna area och volym på följande figur

bredd = 4,0 cm

höjd = 3,0 cm

avfasning = 1,0 cm

hålets diameter = 2,0 cm

• 
• 
  perspektivbild
• 
  framifrån
• 
  från sidan
• 
  uppifrån

14. Ge förslag på mått till en hink som ska rymma 10 liter.

15. Hur hög ska en cylinder som har diametern 5 cm vara om den ska ha samma omkrets som höjd?

C-nivå och A-nivå

16. Vid ett tunnelbygge genom ett berg sprängs ett hål med en diameter på 6 m som är 1,5 km lång. Hur många lastbilslass med sprängsten måste köras bort om varje lastbil kan lasta 20 m³?

17. Då vattnet i ledningarna på natten blivit ljummet över natten vill man spola ur det på morgonen för att man ska kunna få kallt vatten att dricka. Ledningen till kranen är 20 meter lång och har en diameter på 15 mm. En kran med fullt blås spolar ut en liter på 5 sekunder. Hur länge måste man spola innan det kommer kallt vatten?

18. Beräkna volymen på mellanringen i bilden där d1=7,4 mm, d2=14 mm och H=1,6 mm.

19. I en oljepipline flödar olja med en hastighet av 5 m/s. Röret har en diameter på 60 cm. Hur mycket olja rinner per sekund genom pipelinen?

20. Av vilket material tror du en cylinder med måtten ⌀ (diameter) = 25 mm, h = 50 mm är gjord om den väger 66 gram? Kolla på http://sv.wikipedia.org/wiki/Densitet för att se en tabell med några vanliga densiteter.

21. Beräkna volym och area hos följande figur. Radien på den runda biten är precis halva avståndet till kanten. Tjockleken på biten är samma som radien. Antag att radien är r.

22. En Honda transalp har två cylindrar med en diameter på 75 mm. Den totala motorvolymen är 583 cc (cubic centimeters = cm³). Hur lång slaglängd har cylindrarna?

23. Beräkna volym och area hos följande figur (antag att radien är r)

24. Beräkna följande figurs volym

hålet är precis lika stort som innermåtten som är 90 % av yttermåtten. Yttermåtten är en kub med sidan:

a) 4 cm

b) a

25. Om den större och den mindre skivan har samma densitet och den större väger 2 kg, Vad borde då den mindre väga?

Fördjupning

Beräkna area och volym på torusar (munkar/doughnuts).

På Wikipedia finns mer information om torusar: https://sv.wikipedia.org/wiki/Torus

Om

$R$ är avståndet från ringens centrum till själva torusens centrum, och

$r$ är ringens radie

så följer för arean och volymen för en cirkulär torus:

$A=4{\pi }^{2}Rr$

$V=2{\pi }^{2}R{r}^2.$

Ej nivåsatt

Hur mycket rymmer en cylinder som görs av ett kvadratiskt papper som har sidan 20 cm om pappret rullas till ett rör?

En cylinder ska göras av ett A4-papper med måtten 20 cm x 30 cm genom att två delar klipps ut till topp och botten och en del rullas till sidan på cylindern. Sedan tejpas allt ihop. Vad är den maximala volymen man kan få?

Hur mycket skiljer volymen på ett rör som görs av ett papper som rullas på längden jämfört med om det rullas på bredden om det görs av ett papper med måtten

l = 20 cm, b = 30 cm

l = x, b = 2x

Pyramider och koner

$s^2=r^2+h^2$ (Pythagoras sats)

Denna kon är svår att räkna med

Volym

När man ska beräkna volym måste man utgå ifrån basytan (B). Det är den area som är orangefärgad i dessa pyramiderna:

$V=\frac{B\cdot h}{3}$

Denna formel gäller för alla volymer som går mot en spets oavsett hur basytan ser ut så länge som höjden mäts rakt upp fram basytan.

Samma formel gäller till och med så KONstiga koner som i denna bilden (så länge som höjden (h) mäts rakt upp):

Area

För pyramider Måste man beräkna arean på varje sida för sig.

För koner kan arean på struten beräknas med formeln:

$A=\pi \cdot r\cdot s$ (Endast koner)

Övningsuppgifter

Grund-nivå

1. Beräkna volymen på konen. r = 1 cm, h = 4 cm.

2. Beräkna mantelarean på en kon med radien 2 cm och sidan 5 cm.

E-nivå

3. Ge förslag på mått på en kon som har en volym på ungefär 1 dl.

4. Beräkna volymen på en kon med bottendiametern 20 cm och höjden 40 cm.

5. Hur stor del av en kon är fylld om den är fylld till halva höjden?

6. Figuren är 10 cm hög och har en diameter på 4 cm. Beräkna volym och area.

C-nivå och A-nivå

7. En elefantpall är formad som bilden visar. R = 5 dm, r = 3 dm, h = 3 dm.

a) Beräkna pallens sidoarea.

b) Beräkna pallens volym.

8. En trafikkon är 50 cm hög och har bottendiametern 20 cm. Innerdiametern är 18 cm och väggarna är lika tjocka hela vägen. Beräkna vad den väger. Den är gjord av gummi som har en densitet på ca 1 g/cm³.

9. Om man ska fylla en kon till hälften, hur högt i den ska man då fylla?

10. En bubbelpool är formad som en uppochnedvänd kon som är avkapad. Badkarets radie är 60 cm vid bottnen och 80 cm längst upp. Badkaret är 40 cm djupt. Beräkna hur många liter badkaret rymmer.

11. Beräkna figurernas volym (Bilderna är ifrån ett tyskt uppslagsverk från 1800-talet)

a)

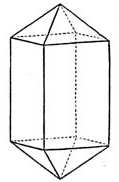
b)

12. Beräkna volym och area hos följande figur

13. Ett prisma är format som bilden visar. Beräkna volymen. (a = 5 cm, b = 3 cm, c = 3 cm, v = 5 cm)

Ej nivåsatt

14. Beräkna pyramiden i bildens volym. Basen är 3 cm och höjden 2 cm.

15. Beräkna volymerna för de olika pyramiderna.

a) Basyta 1 cm², Höjd 5,5 cm.

b) Basyta 2 cm², Höjd 5 cm.

c) Basyta 1,5 cm², Höjd 6 cm.

16. Pyramider kan också vara snea som den här. Basytan är 4 cm² och höjden 3 cm. Beräkna volymen.

17. Beräkna volymen hos denna toppade pyramid.

18. En pyramid ska vara ha kvadratisk bottenyta och vara dubbelt så hög som bred. Beräkna pyramidens bredd för följande volymer

a) 18 cm³

b) 1 liter

c) a cm³

19. Basens sidlängd är 10 cm och höjden är roten ur två gånger så hög. Beräkna volymen.

20. Följande figur är lika hög som bred. Varje kant är 2 cm lång. Beräkna volymen.

21. Beräkna volymen av den gula figuren.

22. Följande figur är 1 cm bred och 3 cm hög. Beräkna volymen.

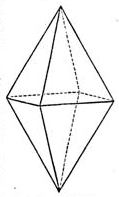
23. Kuben har sidlängden a cm.

a) Ställ upp ett uttryck för kubens volym.

b) Ställ upp ett uttryck för figurens volym.

c) Ställ upp och förenkla andelen som figuren är av hela kuben.

24. Vilken sidlängd ska en pyramid med kvadratisk basyta ha för att

a) Ha samma area som en lika hög kon?

b) Ha samma volym som en kon?

Mall:Matematik för årskurs 7-9/Göm slut

Klot

Volym

$V=\frac{4\cdot \pi \cdot r^3}{3}$

Area

$A=4\cdot \pi \cdot r^2$

Övningsuppgifter

Grund-nivå

1. Beräkna volymen på ett klot som har radien 2 cm.

2. Ett klot har diametern 2 cm

a) Beräkna radien.

b) beräkna volymen

3. Beräkna arean på ett klot med radien 2 cm.

E-nivå

4. Beräkna volymen hos kulan i bilden.

5. En burk är cylinderformad och har höjden och bredden 10 cm.

a) Beräkna burkens volym.

I den burken läggs ett klot som är lika brett och högt som burken så att klotet precis får plats.

b) Beräkna klotets volym.

c) Hur många procent av burkens volym är fyllt av klotet.

6. Vilken av följande himlakroppar har högst medeldensitet

Namn	Radie	Massa
Jorden	637 mil	6,0Mall:E kg
Månen	174 mil	7,3Mall:E kg
Solen	69600 mil	2,0Mall:E kg

7. Hur mycket kan en varmluftsballong lyfta som har diametern 28 m. Densiteten på den varma luften i ballongen är 0,9 kg/m³ och densiteten på luften utanför är 1,2 kg/m³.

8. I ett hagelskott används 32 gram bly som är formade som små kulor med diamtern 3 mm. Hur många kulor är det i varje skott? (Bly har en densitet på 11,34 g/cm³)

9. Vad väger en glaskula med diametern 1 cm? Glas har en densitet på 2,5 g/cm³.

10. Vilken radie har ett klot som har volymen 33,5 cm³?

C-nivå och A-nivå

11. En varmluftsballong är klotformad. Om den behöver kunna lyfta 800 kg, vilken diameter måste den då ha? Kall luft har en densitet på 1,2 kg/m³. Varm luft har en densitet på ca 0,9 kg/m³.

12. En cylinder omsluter exakt ett klot. Hur stor del av cylinderns volym upptas av klotet? Beräkna exakt.

13. Hur mycket större är ett havlklot än en kon om de har samma radie och konens höjd också är samma.

14. Vad har störst volym, ett klot eller den form som blir där tre cylindrar genomskär varandra?

15. Beräkna volymen av den kub där ett åttondels klot har skurits ut som visas på bilden.

16. På ett glasblåseri säljer de glas som är formade som ett halvklot som rymmer ca 20 cl. Nu vill de göra glas formade som koner med samma radie och som rymmer lika mycket. Hur höga bör de glasen vara?

17. I ett hagelskott ska användas 32 gram bly som ska formas till 200 små kulor. Hur stora ska kulorna vara? (Bly har en densitet på 11,34 g/cm³)

Fördjupning

Nått om packning av kulor... Typ:

18. Hur många 1 cm (diameter) kulor får plats i en låda med måtten 8x8x8 cm? Till hur många % är lådan fylld beroende på hur kulorna packas?

Länk: http://en.wikipedia.org/wiki/Sphere_packing

Några olika packningssätt ger för oändligt stora lådor packningsgrader på $\frac{\pi }{\sqrt{18}}\simeq 0.74048.$(bäst), $\frac{\pi }{6}$, $\frac{\pi }{3\sqrt{3}}$ och $\frac{\pi \sqrt{3}}{16}$.

Detta är viktigt när man studerar kristaller. När man studerar hur mycket grus eller malm man kan packa i en lastbil används slumpmässig packning som brukar bli ca 64% men att räkna med det är mycket mer komplicerat.

Ej nivåsatt

19. Hur många gånger större är ett klots hela area än dess genomskärningsarea?

20. Hur hög ska en låda som precis rymmer ett klot vara för att ha samma volym som klotet? Klotet kommer alltså inte få plats på höjden i lådan.

21. Beräkna volymen av en apelsinklyfta. (Kanske bättre som disskussionsuppgift?)

22. Beräkna volym och area på följande lilla kula

23. Kulorna i bilden är 1, 2, 5, 10 och 20 mm i diameter. Hur många av de olika små måste man smälta ihop för att få tillräckligt för att göra en stor?

24. Kulan på bilden är 60 mm i diameter. Vad borde kräva mest putsmedel, att putsa den eller att putsa ena sidan på en 10 cm x 10 cm stor kvadrat av samma material?

En julgranskula är 5 cm i diameter. Den är gjord av 4 cm³ plast. Hur tjocka är kulans väggar? Prova dig fram eller använd tredjeroten om du kan.

26. Mer bilder att använda till uppgifter

Blandade figurer

Övningsuppgifter

E-nivå

1. Solens diameter är ca 1 392 000 km och dess massa är ca 1,9891 ⋅ 10³⁰ kg. Beräkna solens densitet.

Ej nivåsatt

2. Beräkna area och volym på följande figurer

a)

Längd: 3

Diameter: 2

b)

Kubens sida = halvklotens diameter: 2

c)

Längd: 4

Diameter: 2

d)

Längd = bredd: 4

Tjocklek: 2

e)

ytterradie: 1

innerradie: 0,9

Mall:Matematik för årskurs 7-9/Lösning

3. Hur hög ska en cylinder vara för att ha samma volym som ett klot om de har samma radie. Svara exakt.

4. Hur hög ska en kon vara för att ha samma volym som ett halvklot om de har samma radie. Svara exakt.

5. Beräkna förhållandet mellan area och volym på

a) en kub med sidan 1 cm

b) en cylinder med diametern och höjden 1 cm

c) ett klot med diametern 1 cm

6. Beräkna förhållandet mellan area och volym på

a) en kub med volymen 1 cm³

b) en cylinder med samma diameter och höjden och volymen 1 cm³

c) ett klot med volymen 1 cm³

7. En kon har bottenradien 2 cm och höjden 4 cm.

a) Beräkna dess volym.

b) Om den är fylld till halva höjden, vad är dess volym då?

c) Vilken höjd ger en hälften så stor volym som i a-uppgiften?

Övrigt

Geometriövningar i google sketchup, geonext, geogebra, för hand, med passare?

Eller ska de läggas som en egen sida som bara länkas in här?

Länkar

• Google sketchup
• Geonext
• GeoGebra.
• m.fl.